Kendrick

Prelude

For the past few months I've been working with the Ethereum Foundation on a Minimal Anti Collusion Infrastructure (MACI) project that utilises zero knowledge proofs. Working on this project has been technically challenging and thorougly enjoyable but not without some difficulties. As the main form of communication between collaborators were through google hangouts / signal calls, there existed an issue where concepts were unable to be interpreted in the intended way they were expressed, due to pitfalls of spoken word and the varied terminology used for the same concept.

In an effort to express what words cannot, this blog post will visualise the implementation of merkle trees (specifically a simplified version of the audited semaphore merkle tree), the primary data structure used throughout the MACI project.

Note: This post assumes you understand what a hash function is.

Introduction

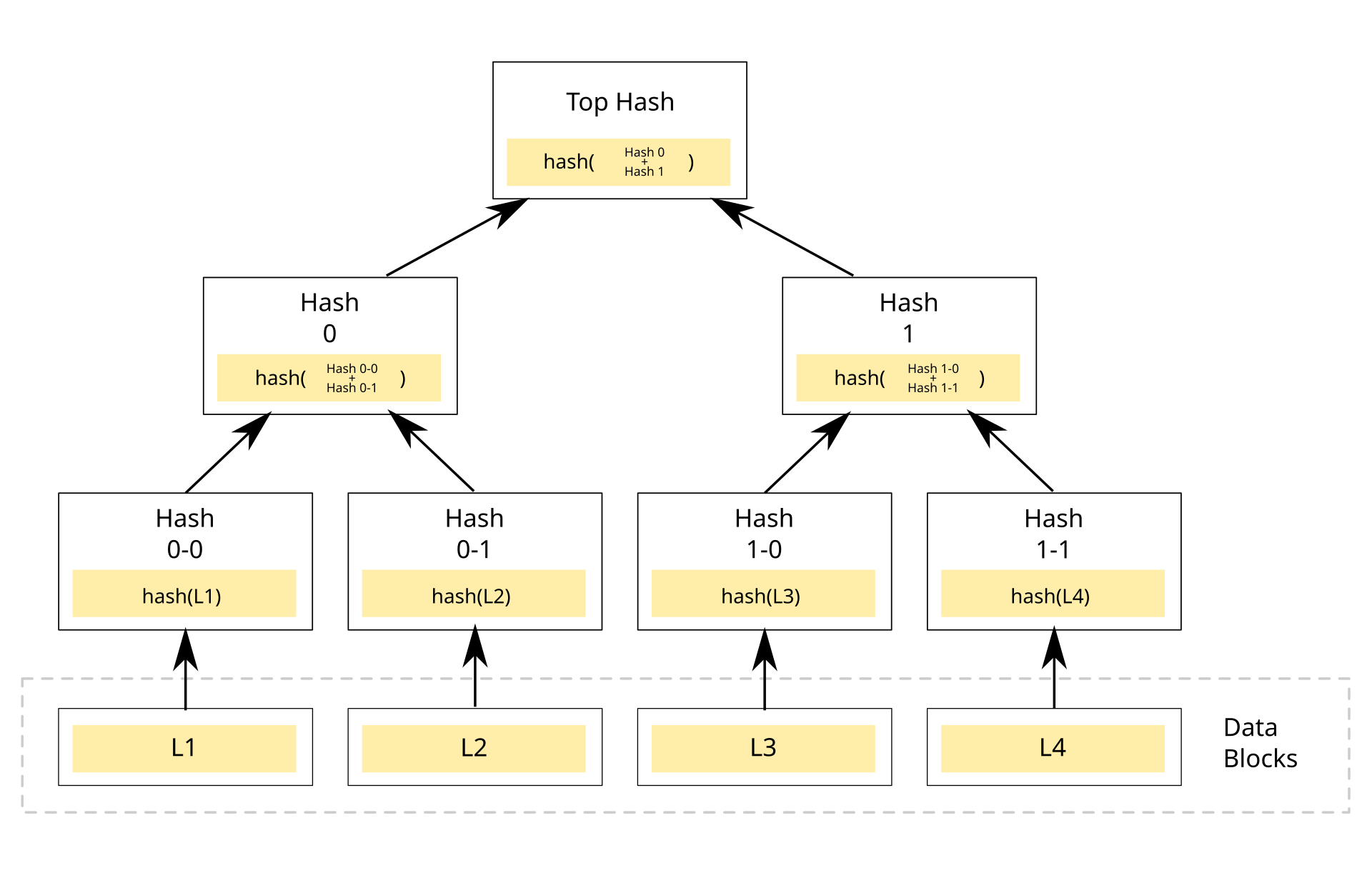
Figure 1: Merkle tree visualization, source: brilliant.org¹

The data structures ultilized when building zero-knowledge proof applications on the blockchain have to be time efficient due to the limitations of both the zero knowledge circuit compiler(s) and blockchain VM(s).

Merkle trees, a type of data structure is great for this use case as they can be used to verify whether some data exists in the tree very efficiently, as even at worse case, time complexity is linear¹. Their strong data verification properties are also perfect for our need of being able to prove something without revealing what that particular something is.

Figure 1 shows a merkle tree with a depth of 2, giving us 4 (2^N, where N is the depth) data blocks to store our data (a merkle tree can have an arbitrarily depth of N). As shown in the figure, each pair of data block is hashed with some arbitrary hash function recursively until we reach the final root value. This root value is significant as it represents the hashes of all previous values, and with that root value, we can use it to proof if some data exists within the tree.

Merkle Tree Overview

I personally understand the rationale behind technical implementations quicker once I've used them, and so I would like to start off by showing some code examples on how one might:

1. Create a merkle tree
2. Insert a leaf into the merkle tree
3. Update a leaf in the merkle tree
4. Verify if some leaf exists in the merkle tree

You can also play around with the tool used to create most of the visuals here at efficient-merkle-trees.netlify.com.

1. Creating A Merkle Tree

const bigInt = require('big-integer')
const { createMerkleTree } = require('./src/utils/merkletree.js')

const depth = 3
const zeroValue = bigInt(0)

const merkleTree = createMerkleTree(depth, zeroValue)

Figure 2: Merkle Tree With Depth 3

The zeroValue is the placeholder/default value of the leaves of the merkle tree and is needed as we still need to be able to compute a root value of the merkle tree regardless of how filled it is. This initialization with the default zeroValue can be seen in Figure 2 above.

2. Inserting A Leaf

merkleTree.insert(bigInt('7ff', 16))

for (let i = 1; i <= 7; i++) {
  merkleTree.insert(i)
}

Animation 1: Merkle Tree Insertion Example

Notice how in Animation 1 above, the top-most root value always changes whenever a new leaf is inserted. In a way you can preceive the root value as a sort of ‘representation’ of all the leaves within the tree.

This is an important feature where we can prove some data exists in the tree, without revealing that particular piece of data.

Note: The leaf with the green-ish outline is the latest inserted value.

3. Updating an Existing Leaf

const leafIndex = 1

for (let i = 2; i <= 7; i++) {
  const [path, _] = merkleTree.getPathUpdate(leafIndex)
  merkleTree.update(leafIndex, i, path)
}

Animation 2: Merkle Tree Update Example

To update an existing leaf in the merkle tree, we first need to get its path values, which are determined by the existing leaf's index. The path values are the minimal values required to reconstruct the root value.

More intuitively, the path values are the root/leaf values that don't get affected when you update the existing leaf's value, and is outlined in yellow orange in Animation 2 above.

e.g. For leaf index 1 (which consists of value 0x1), the path values are 7fff, 2fbb8b67f32aef36e17419a299baac1b12f466a02c7984b5781089ed35a74c23, 103566ca66f0f2dbd35ebc5f94905c71c28b9d9230d141ea5cb0f71f09580535

Given that we know the path values to reconstruct the tree, we can conclude the time complexity is O(n) (where n is the depth of the tree) for both the average and worse case scenario¹.

If you would like to remove some data from the merkle tree, you could simply update the index of the leaf to the zeroValue defined when the tree was created.

4. Verifying Arbitrary Data

4.1 Verifying Data Exists in Merkle Tree

const { hash } = require('./utils/merkletree')

const leafIndex = 3
const dataToVerify = bigInt(3)

const [path, _] = merkleTree.getPathUpdate(leafIndex)
const isValid = merkleTree.leafExists(leafIndex, dataToVerify, path)

console.log(`Data exists: ${isValid}`)
// Data exists: True

Animation 3: Proving Some Data Exists In Merkle Tree

Just like how we require the path values to update an existing tree in the merkle tree, we can also use the same path values to recursively hash the data we want to prove exists in the tree until we obtain a final tree root. If the final obtained tree root is identical to the reference tree root, we know that the data does exist in the tree.

1. Alice and Bob both have constructed identical merkle trees.
2. Bob wants to prove to Alice that they both have identical merkle trees.
3. Bob provides Alice with his path values, merkle tree root, and the index used to obtain the path values.
4. Should Alice use the leaf value at index from her merkle tree, and recursively hash with the path values from Bob to achieve an identical merkle tree root, then they both have an identical merkle tree.

The process of recursively hashing a supplied leaf with the path values can be seen in Animation 3 above, where the supplied leaf in that case is 3, and the path values are the boxes outlined in yellow orange.

4.2 Verifying Data Does Not Exists in Merkle Tree

const { hash } = require('./utils/merkletree')

const leafIndex = 3
const dataToVerify = bigInt(102934018234802841028) 

const [path, _] = merkleTree.getPathUpdate(leafIndex)
const isValid = merkleTree.leafExists(leafIndex, dataToVerify, path)

console.log(`Data exists: ${isValid}`)
// Data exists: False

Animation 4: Proving Some Data Does Not Exist In Merkle Tree

Conversely, if we use a leaf value that does not exist in the tree and recursively hash it with the path values, we will obtain a different merkle tree root. This is shown in Animation 4 above.

Conclusion

By using merkle trees, we are able to construct a “compressed” representation of an arbitrary set of data that allows us to efficienty prove the existence of some data in the tree in logarithmic time (relative to the set of data, as our path values will always be log2(K) length long, where K is the length of the set of data, NOT the depth of the merkle tree).

Again, you can also play around with the tool at efficient-merkle-trees.netlify.com.

Tl;dr: Merkle trees good, make slow compute faster.